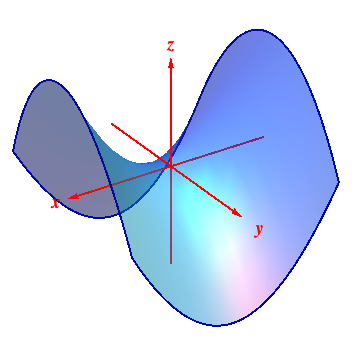
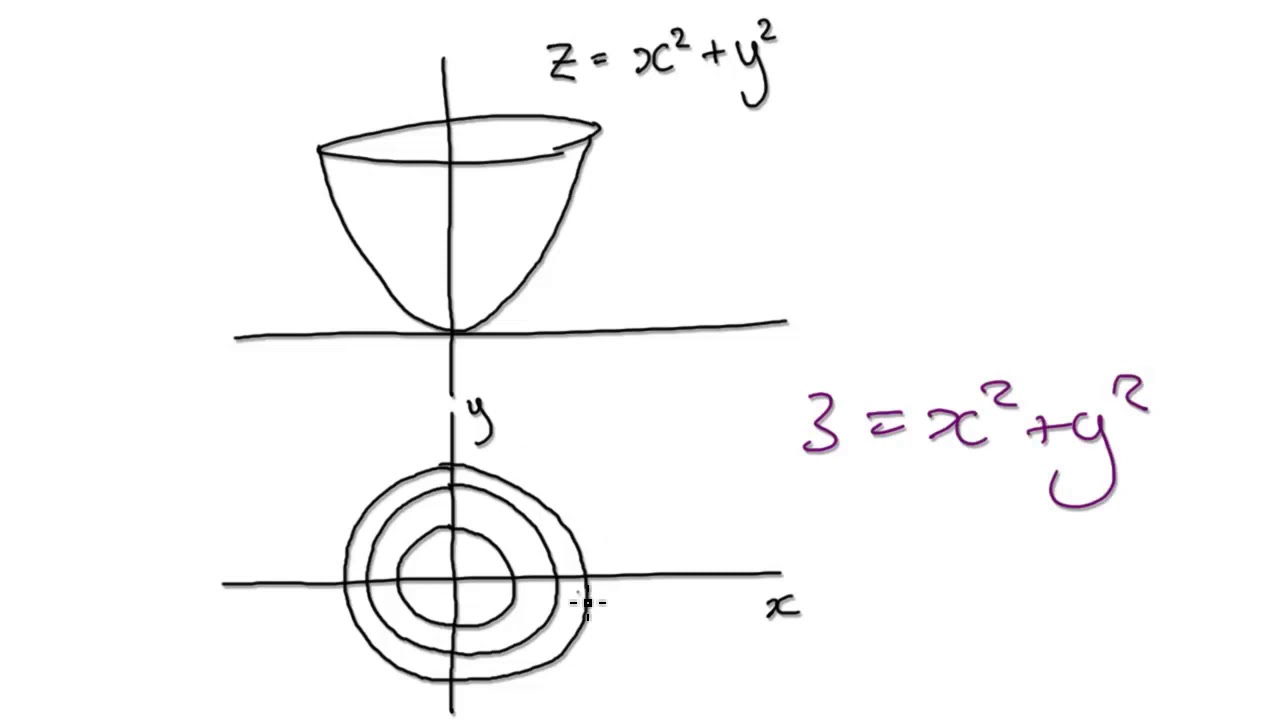
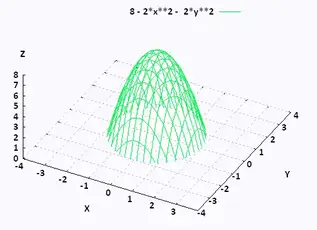
Calc 3 Level curves Close 1 Posted by 6 years ago Archived Calc 3 Level curves Let k(x,y)= 4x 2 8x 5y 2 3 Sketch the level curves for c= 1, 15, and I got a hyperbola from this, but now I'm in doubt because one of the values of c make it undefined Is this possible?When drawing in three dimensions is inconvenient, a contour map is a useful alternative for representing functions with a twodimensional input and a onedimensional outputSo again, we want to try to do visualize the level surfaces dysfunction And so you could pick anything you wanted Let's say we picked K equaling zero In other words, on the set of all points X y Z, for which the output of the function is zero So zero is equal to Z squared minus X squared, minus y squared

A Find The Function S Domain B Find The Function S Range C Describe The Function S Level Curves D Find The Boundary Of The Function S Domain E Determine If The Domain Is An Open
Level curves calc 3
Level curves calc 3-413 Sketch several traces or level curves of a function of two variables 414 Recognize a function of three or more variables and identify its level surfaces Our first step is to explain what a function of more than one variable is, starting with functions of two independent variables This step includes identifying the domain and range of · The 3D Coordinate System – In this section we will introduce the standard three dimensional coordinate system as well as some common notation and concepts needed to work in three dimensions Equations of Lines – In this section we will derive the vector form and parametric form for the equation of lines in three dimensional space We will also give the symmetric



How Do You Sketch Level Curves Of Multivariable Functions Vector Calc Vector Calculus Calculus Math
Related Documents Acoustic Calculation of · Check for values that make radicands negative or denominators equal to zero Functions of two variables have level curves, which are shown as curves in the However, when the function has three variables, the curves become surfaces, so we can define level surfaces for functions of three variables DefinitionJust as having a good understanding of curves in the plane is essential to interpreting the concepts of single variable calculus, so a good understanding of surfaces in $3$space is needed when developing the fundamental concepts of multivariable calculus We've already seen surfaces like planes, circular cylinders and spheres
Help you understand some of the level curves of the function, and (b) use the computer to graph (a portion of) the surface z = g(x, y) In addition, mark on your surface some of the contour curves corresponding to the level curves you obtained in part (a) (See Figures 210 and 211) g(x, y) = yex 21 2 1x2y g(x, Y) = 22Directional derivatives and Gradient;Gradient vector and level curves The gradient vector of a function of two variables, evaluated at a point (a,b), points in the direction of maximum increase in the function at (a,b) The gradient vector is also perpendicular to the level curve of the function passing through (a,b) Below is the graph of the level curve of the function
Calc 3 lagrange multiplier example 1;Related Topics Acoustics Room acoustics and acoustic properties decibel A, B and C Noise Rating (NR) curves, sound transmission, sound pressure, sound intensity and sound attenuation;Level 3 Calculus, 16 930 am Wednesday 23 November 16 FORMULAE AND TABLES BOOKLET for , and Refer to this booklet to answer the questions in your Question and Answer booklets Check that this booklet has pages 2 – 4 in the correct order and that none of these pages is blank


Surfaces And Traces



How Do You Sketch Level Curves Of Multivariable Functions Vector Calculus 2 Youtube
Sect 151 & 152 (Graphs & Level Curves & Limits & Discontinuity) MATH 2421 Kawai Sect 151 (Graphs & Level Curves) 1 So far, we™ve seen a bunch of 3D surfaces In the same way that there are an in–nite number of 2D curves, we should decide which ones are functionsLevel Curves and Level Surfaces Line Integrals Optimization and Related Rates Optimization for Functions of 2 Variables Parametric Equations 2space Parametric Equations 3space Partial Derivatives Polar Coordinate System Polar Coordinates Derivatives and Integrals PreCalculus Riemann Sums and the Fundamental Theorem of Calculus 2d order Diff EQSMotionCalculus 3 Lecture 131 Intro to Multivariable Functions (Domain, Sketching, Level Curves) Working with Multivariable Functions with an emphasis on findi


Multivariable Calculus F X Y X Ln Y 2 X Is A Function Of Multiple Variables It S Domain Is A Region In The Xy Plane Ppt Download



Problems On Surfaces Calc 3 I Do Not Understand Chegg Com
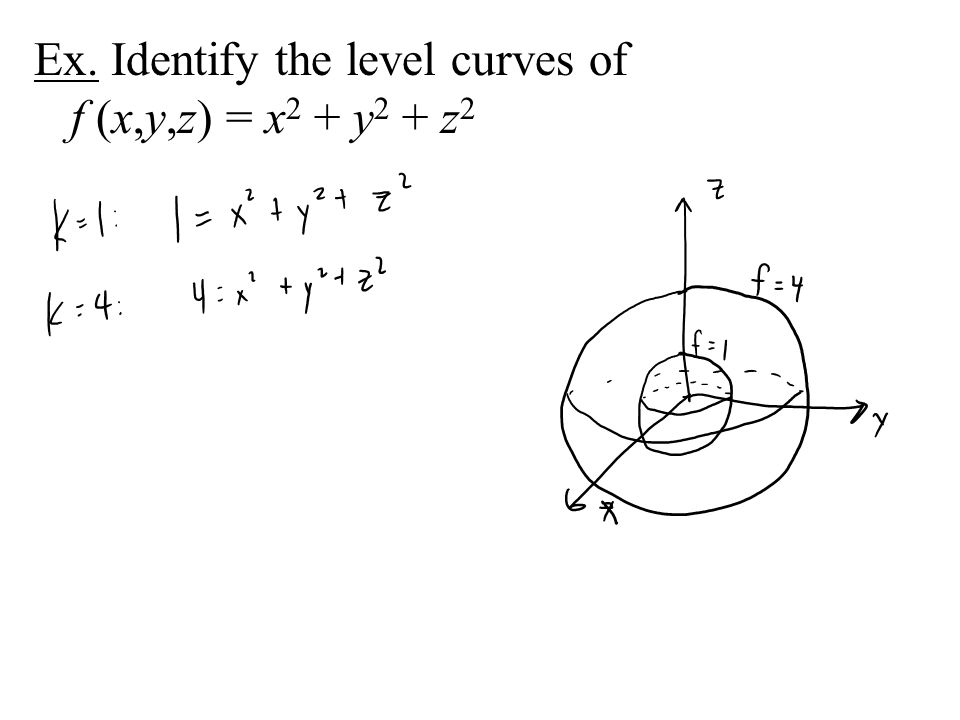
Absolute max and min on closed and bounded set;Unit 3 Multiple Integration Riemann Sums of a Double Integral1 Level Surfaces 2 If one of the Arguments is time we can animate ie w = f(x,y,t) Level Surfaces Given w = f(x,y,z) then a level surface is obtained by considering w = c = f(x,y,z) The interpretation being that on a level surface f has the same value at every pt For example f could represent the temperature at each pt in 3space



Level Curves And Cross Sections Maple Programming Help


Contour Maps Article Khan Academy
A lecture on level curves, partial derivatives, and tangent planes The beginning of a study of functions of several variables Math Vids offers free math help, free math videos, and free math help online for homework with topics ranging from algebra and geometry to calculus and college mathCalc 3 level sets review example;Study guide and practice problems on 'Level curves and surfaces'


Contour Maps Article Khan Academy


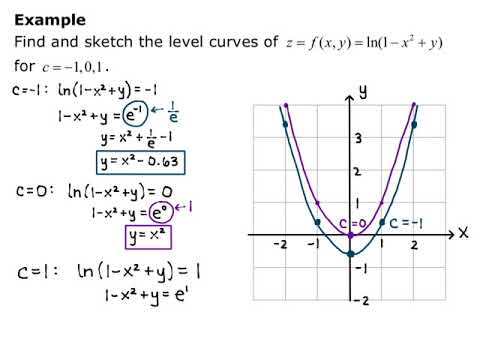
Calculus Iii Functions Of Several Variables
The level curves f(x,y) = k are just the traces of the graph of f in the horizontal plane z=k projected down to the xyplane Figure 1 Relation between level curves and a surface k is variating acording to 5015 One common example of level curves occurs in topographic maps of mountainous regions, such as the map in Figure 2 The level curves are curves of constant elevation of theMain Concept A level curve of the surface is a twodimensional curve with the equation , where k is a constant in the range of f A level curve can be described as the intersection of the horizontal plane with the surface defined by f Level curves are also known as contour linesPartial derivatives Quiz 7 Tangent planes;


Labware Ma35 Multivariable Calculus Two Variable Calculus


Section 13 1 Level Curves Youtube
I need help finding the domain and the range of this function, I was thinking that the range could be (0,Infinity) but I'mQuiz 3 key Quiz 4 key Quiz 5 key Quiz 6 key Quiz 7 key Quiz 8 key Quiz 9 key Quiz 95 key Quiz 10 key Quiz 11 key Quiz 12 key Quiz 13 key Quiz 14 key Quiz 15 key Quiz 16 key Quiz 17 key Quiz 18 key Exam 1 materials Preparation Sheet for Exam 1 multivariatepdf surface plot, traces and level curvesQuestion Webassignnet UTILASS MY NOTES AS DETAILS 3 /1 Points LARCALC11 Describe The Level Curves Of The Function Z = 12 3x 4y, C = 0, 2, 4, 6, 8, 10 The Level Curves Are Parabolas The Level Curves Are Circles The Level Curves Are Noncircular Ellipses The Level Curves Are Parallel Lines The Level Curves Are Hyperbolas



Solved Calculus 3 Find And Sketch The Domain Of The Foll Chegg Com
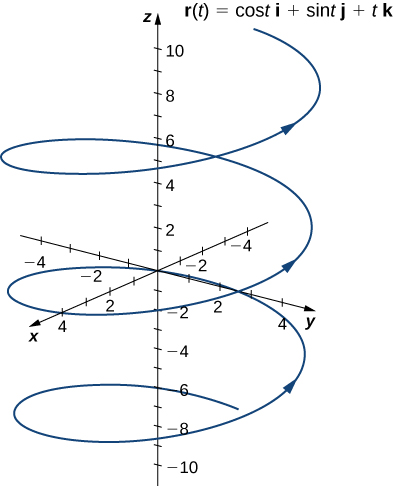


Vector Valued Functions And Space Curves Calculus Volume 3
LEVEL CURVES The level curves (or contour lines) of a surface are paths along which the values of z = f(x,y) are constant;Noise and Attenuation Noise is usually defined as unwanted sound noise, noise generation, silencers and attenuation in HVAC systems;Calc 3 level sets review question part 2;



Level Curves Mit 18 02sc Multivariable Calculus Fall 10 Youtube



Cal123 Level Curves And Contour Diagrams Contour Line Curve
» Clip Level Curves and Contour Plots () From Lecture 8 of 1802 Multivariable Calculus, Fall 07 Flash and JavaScript are required for this featureLearning module LM 121 3dimensional rectangular coordinates Learning module LM 122 Vectors Learning module LM 123 Dot products Learning module LM 124 Cross products Learning module LM 125 Equations of Lines and Planes Learning module LM 126 Surfaces Surfaces and traces Level curves Level surfaces Worked problemsQuiz 6 Multivariable functions;



Calculus Iii Functions Of Several Variables



How To Find The Level Curves Of A Function Calculus 3 Youtube
Major Ideas in Calc 3 / Exam Review Topics s Know how to graph level curves of a function of 2 variables, and how to graph level surfaces of a function of 3 variables s Be able to connect the graph of a function of several variables with the graph of its level sets, and be able toThe level curves of f(x,y) are curves in the xyplane along which f has a constant value · 1624 // Summary for how to sketch level curves Whenever you're dealing with a multivariable function, the graph of that function will be a threedimensional figure in space If you take a perfectly horizontal sheet or plane that's parallel to the xyplane, and you use that to slice through your threedimensional figure, then what you get at the intersection of the figure and the



A Find The Function S Domain B Find The Function S Range C Describe The Function S Level Curves D Find The Boundary Of The Function S Domain E Determine If The Domain Is An Open



How To Find The Level Curves Of A Function Calculus 3 Youtube
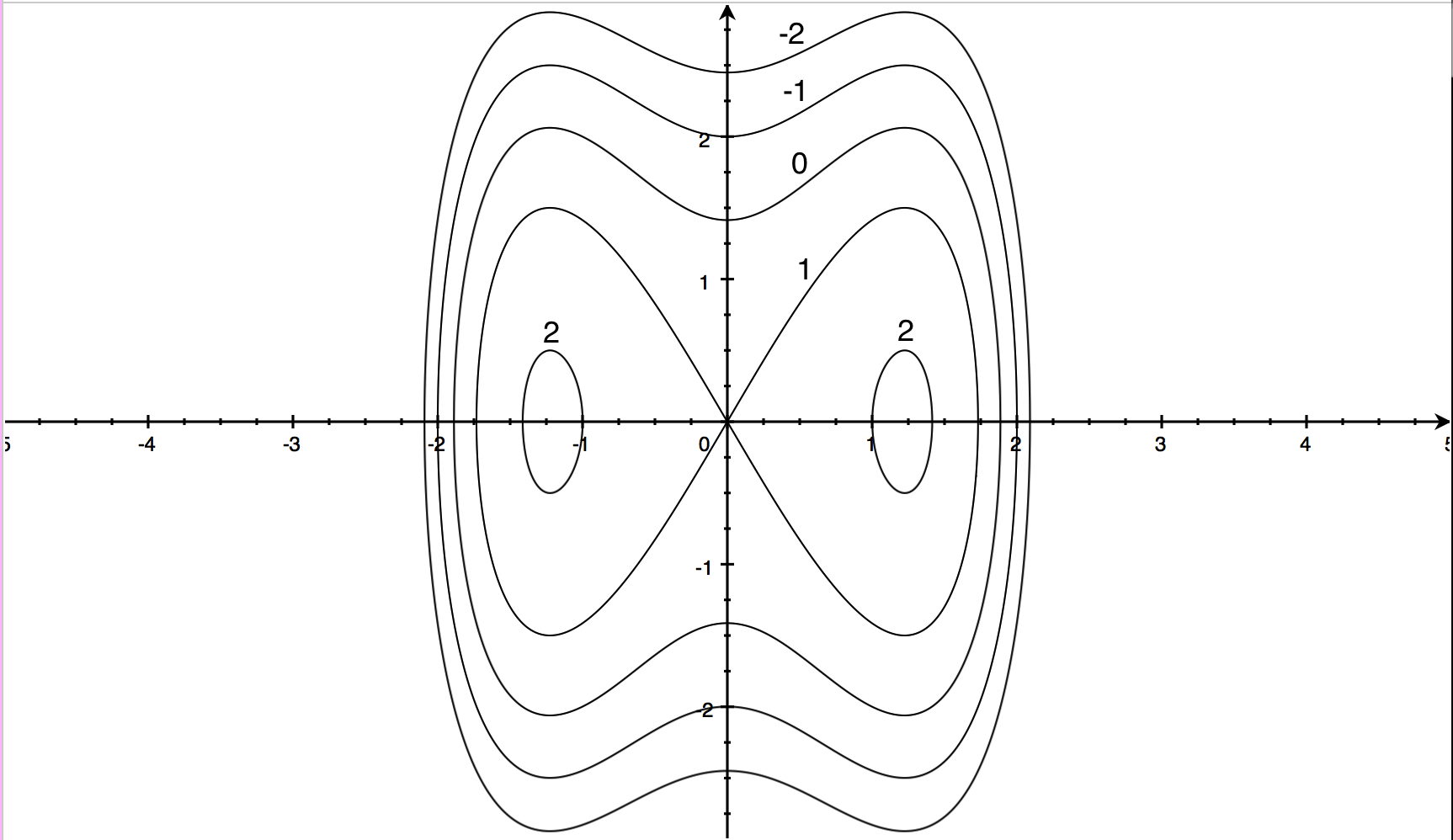
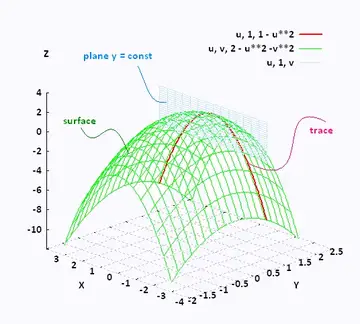
Calc 3 Level Curves University/College Student (Higher Education) Close Vote Posted by University/College Student (Higher Education) just now Calc 3 Level Curves University/College Student (Higher Education) Hi!As David Hu mentioned, there are differences at different schools, but here's an outline of what my university teaches for Calculus 3 (ordered a little differentlyIe the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curves of the function



Calc 501 1000 By James Bardo Issuu


12 1 Introduction To Multivariable Functions Mathematics Libretexts
Calc 3 The oracle function f(x,y) is presented below For each point (x,y) you enter the oracle will tell you the value f(x,y) Estimate the partial derivative of the function at (16,−) using the Newton quotient definition Calc 3 The figure below shows some level curves of a differentiable function f(x,y)SeaLevel Curve Calculator (Version 1921)Calc 3 constrained min max problem ;



Level Set Examples Math Insight
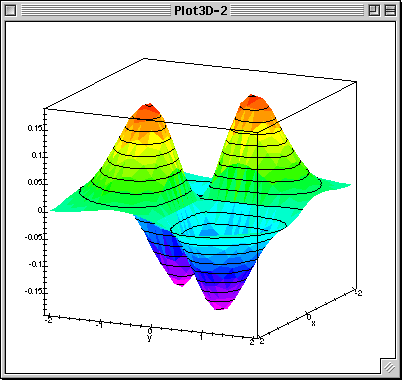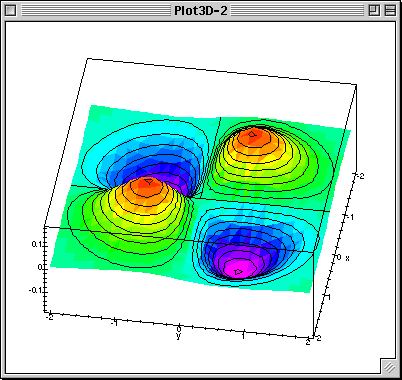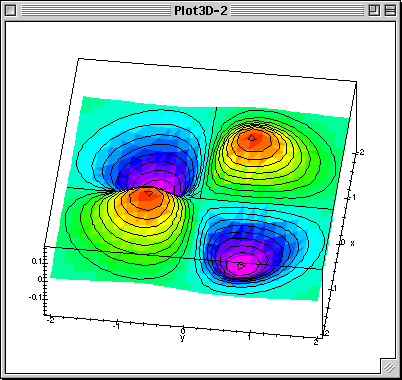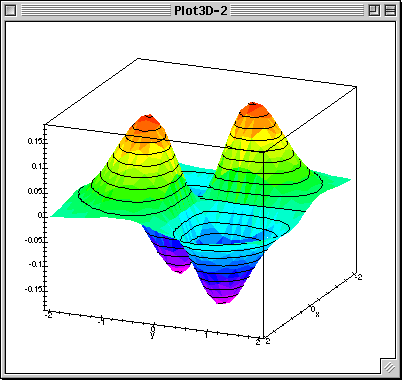


Multivariable Calculus Course Homepage
Analysis Parameter u is the height z of a contour, so take the first two equations for a fixed value of u, eg ParametricPlot{125 Cosv, 125 Sinv}, {v, 0, 2 Pi} whose result, not shown here, is the expected circle Implementation For several heights, apply a function with the height as argument to a list of those heights, producing a list of individual circular images;113 Level Curves Imagine stepping onto a surface and walking along a path with constant elevation The path you walk on is known as the contour curve, while the projection of the path onto the xyplane is known as a level curve 6 12 Limits and Continuity 121 LimitsExplanation There are several ways to solve this problem, but the most effective would be to notice that we can derive the followingHence Therefore our curve is a circle of radius , and it's circumfrence is But we are only interested in half that circumfrence ( is from to , not ), so our answer is Alternatively, we could've found the length using the formula



Gradients And Level Curves Youtube



012 Sketching Level Curves Of Multivariable Functions Pdf Docer Com Ar
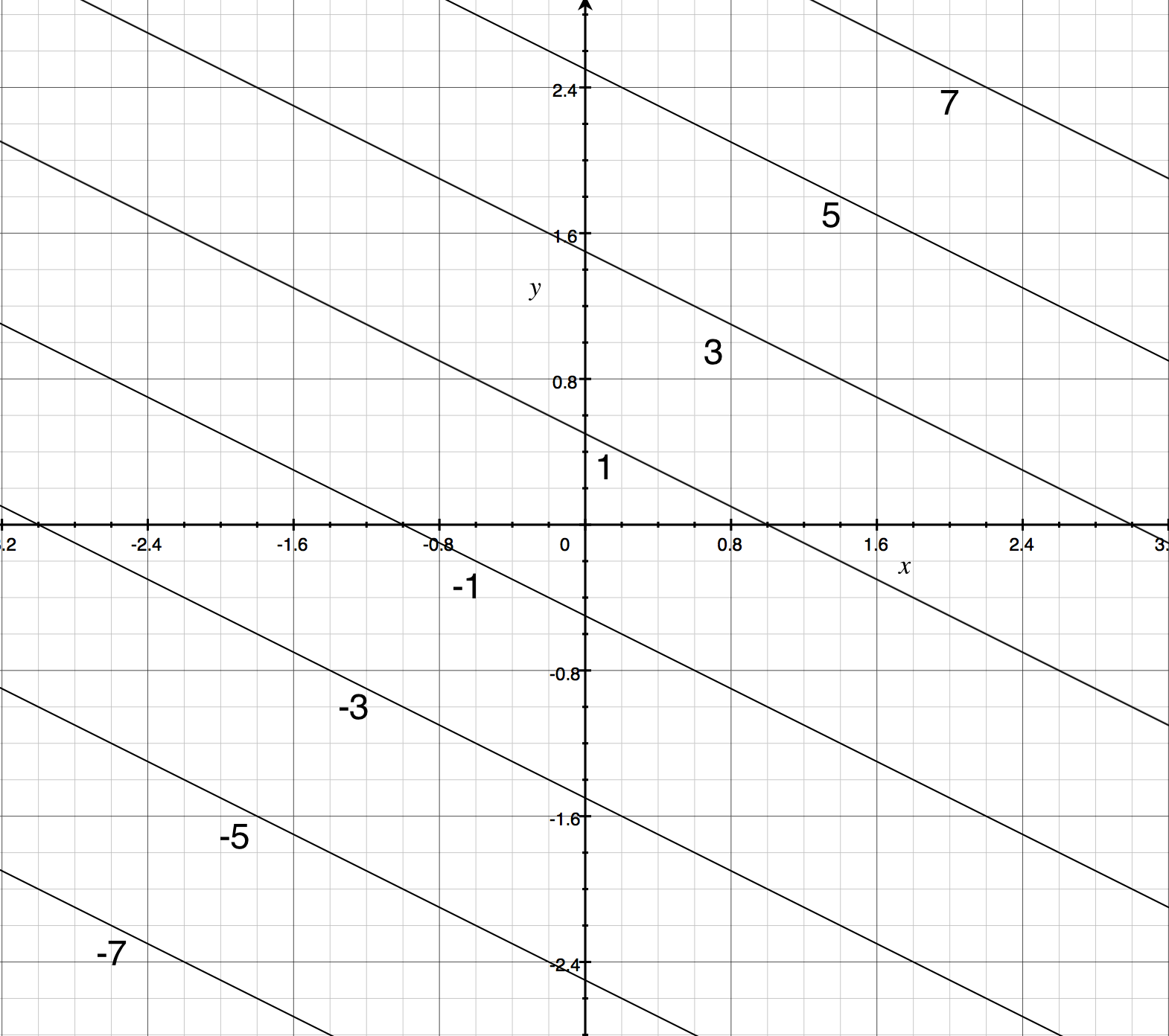
97 · h 3 (P) = f(P)g(P) h 4 (P) = f(P)/g(P) Then, h 1 (P), h 2 (P), h 3 (P), and h 4 (P) (when g(P) is not equal to zero) are all scalar fields,too (they take in a point P in space and return a scalar) Level Curves Level Curves are a tool for understanding and expressing the basic nature of two variable functions Say we want to get a visual feel · How to Find the Level Curves of a Function Calculus 3 How to Find the Level Curves of a Function Calculus 3 Watch later Share Copy link Info Shopping Tap toCalculus for Scientists and Engineers Early Transcendental Level curves of planes Prove that the level curves of the plane a x b y c z = d are parallel lines in the x y plane, provided a 2 b 2 ≠ 0 and c ≠ 0 Functions of Several Variables Graphs and Level Curves



Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
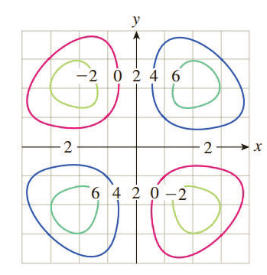


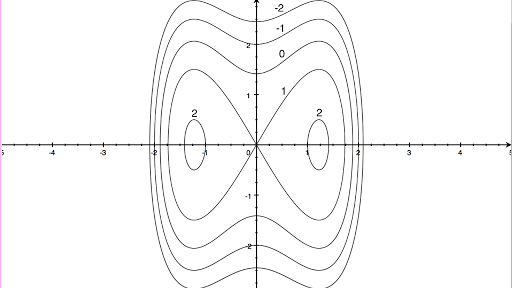
Exercises 55 58 Refer To The Following Plot Of Some Level Curves Of F X Y C For C 2 0 2 4
· So the equations of the level curves are \(f\left( {x,y} \right) = k\) Note that sometimes the equation will be in the form \(f\left( {x,y,z} \right) = 0\) and in these cases the equations of the level curves are \(f\left( {x,y,k} \right) = 0\) You've probably seen level curves (or contour curves, whatever you want to call them) before · I got lucky in Calc 3 and my instructor let us use graphing software on the exams, so I always graphed the regions in Geogebra Made it so much easier to set your bounds when you can actually see the shape you're integrating over I had friends in another class that had to do level curves if they wanted to determine the shape RIPThe level curves of $f$ is the set $$ \{ (x,y) \in \mathbb{R}^2 f(x,y) = K, K \in \mathbb{R} \}$$ So, in order to find the level curves of your function, just set it equal to a



Level Curves


Video3144 Calculus 3 Introduction To Level Curves Youtube
Example 1312 Graph the projections of $\langle \cos t,\sin t,2t\rangle$ onto the $x$$z$ plane and the $y$$z$ plane The two dimensional vector function for theAlso, is it really a hyperbola?A level set of a function of three variables $f(x,y,z)$ is a surface in threedimensional space, called a level surface Level curves One way to collapse the graph of a scalarvalued function of two variables into a twodimensional plot is through level curves A level curve


Calculus Iii Vector Functions



Calculus Iii Functions Of Several Variables
· We can use this theorem to find tangent and normal vectors to level curves of a function Finding Tangents to Level Curves For the function find a tangent vector to the level curve at point Graph the level curve corresponding to and draw in and a tangent vectorThere are actually two ways to enter and graph the level surface equations for a particular function of three variables in CalcPlot3D Solve each equation for \(z\) in terms of \(x\text{,}\) \(y\text{,}\) and \(C\) and enter the level surface using one or two functions of \(x\) and \(y\text{,}\) orDirectional derivatives Quiz 8 Taylor polynomials;



College Freshman Calculus Multivariable Calculus 3 Gradient Lines And Directional Derivatives Homework 53 Homeworkhelp



Level Surfaces
Level curves calc 3 provides a comprehensive and comprehensive pathway for students to see progress after the end of each module With a team of extremely dedicated and quality lecturers, level curves calc 3 will not only be a place to share knowledge but also to help students get inspired to explore and discover many creative ideas from themselvesLevel Curves (Braxton Carrigan) Level Curves;



How To Graph The Domain Of Question 11 Calculus
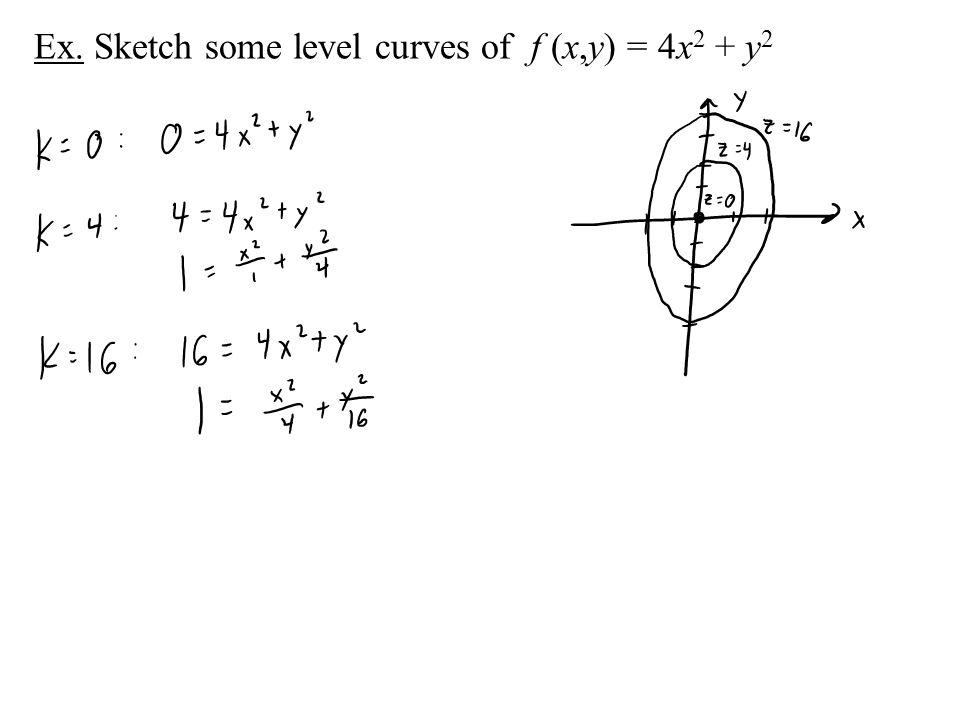


Multivariable Calculus F X Y X Ln Y 2 X Is A Function Of Multiple Variables It S Domain Is A Region In The Xy Plane Ppt Download



Solved Calculus Iii Hw 5 Due Weds Feb 21 4 Pts Each N Chegg Com



Session 35 Gradient Definition Perpendicular To Level Curves Part B Chain Rule Gradient And Directional Derivatives 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



How To Sketch Level Curves Vector Calculus Youtube



How Does One Project The Gradient At A Point On A Surface Into A Plane Mathematics Stack Exchange
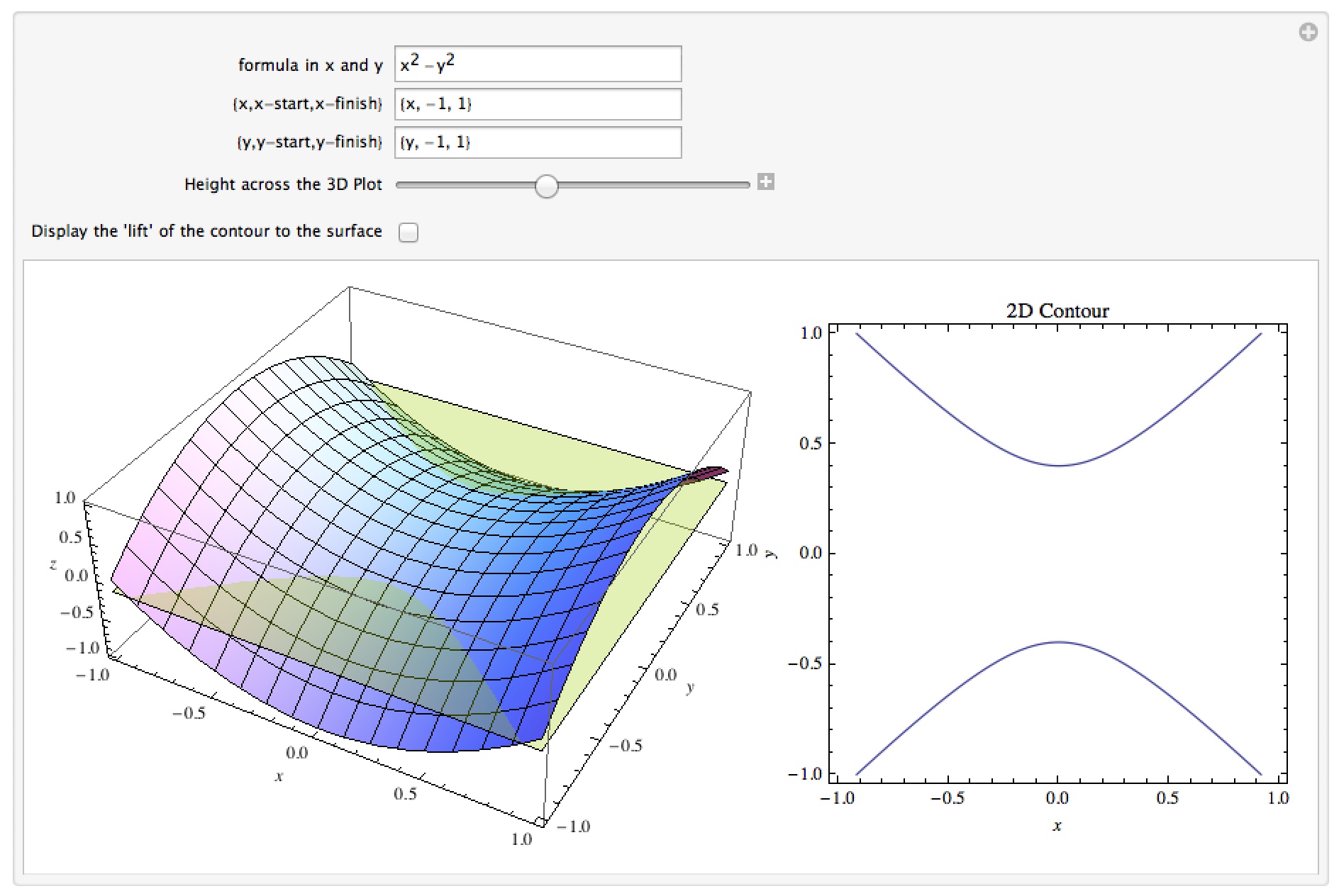


Dr Moretti S Mathematica Notebooks Calculus 3



Lagrange Multipliers Calculus And Analytical Geometry Notes Math c Docsity


Oql1pw9xmctx6m



Solved 4170 Qui Quiz 3 Calculus Iii Spring Name 1 Chegg Com



9 Questions Sample Exam 3 Calculus Ii Math 116 Docsity



Calc Iii Contour Map Level Curves Youtube



Mat251 Multivariable Calculus Iii Name Prof Porter



Level Curves



Calculus Iii The Dot Product Level 7 Examples V Calculus Graphing Dots



How To Sketch Level Curves Youtube



Solved Sketch The Level Curves Of The Function G X Y Chegg Com



How Do You Sketch Level Curves Of Multivariable Functions Vector Calculus 3 Youtube


Oql1pw9xmctx6m



Calculus Iii



Level Sets Math Insight



Level Sets Math Insight


Latex Pictures



Calculus Iii Functions Of Several Variables



Calculus Iii Functions Of Several Variables


Contour Maps Article Khan Academy
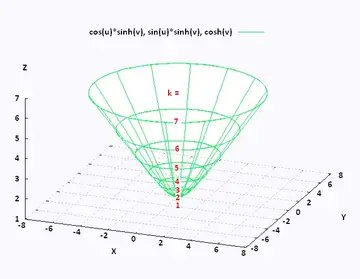


Oql1pw9xmctx6m
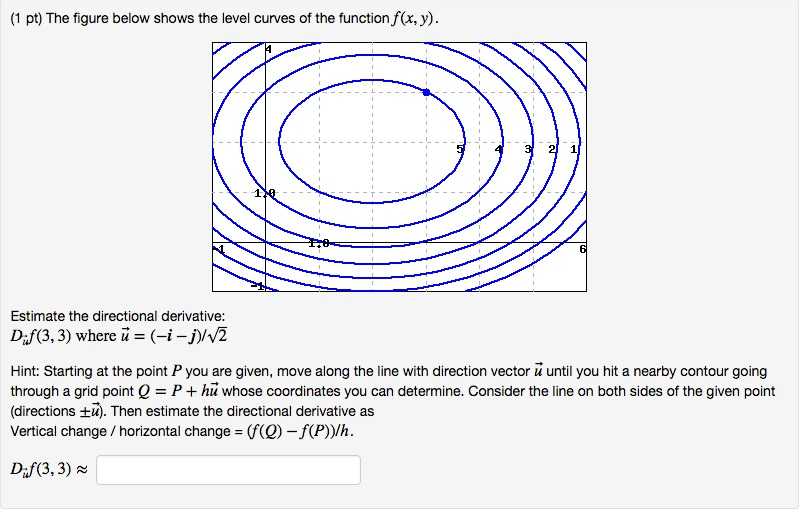


Solved The Figure Below Shows The Level Curves Of The Fun Chegg Com



Multivariable Calculus Johns Hopkins Center For Talented Youth
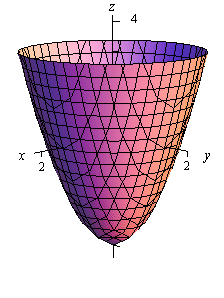


Calculus Iii Functions Of Several Variables



Calc 3 Cheat Sheet Mathematical Analysis Space



How Do You Sketch Level Curves Of Multivariable Functions Vector Calc Vector Calculus Calculus Math
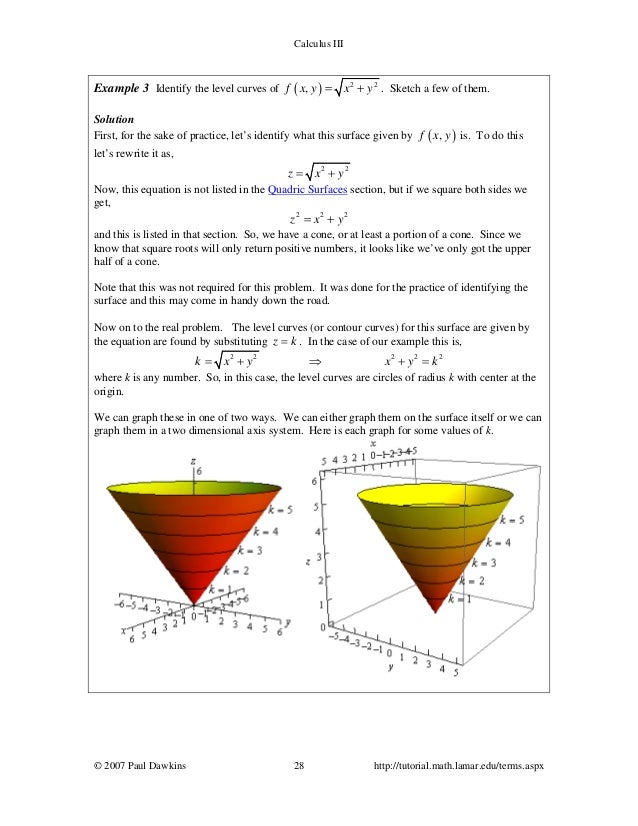


Calkulus Iii Complete



Level Surfaces



Multivariable Calculus F X Y X Ln Y 2 X Is A Function Of Multiple Variables It S Domain Is A Region In The Xy Plane Ppt Download
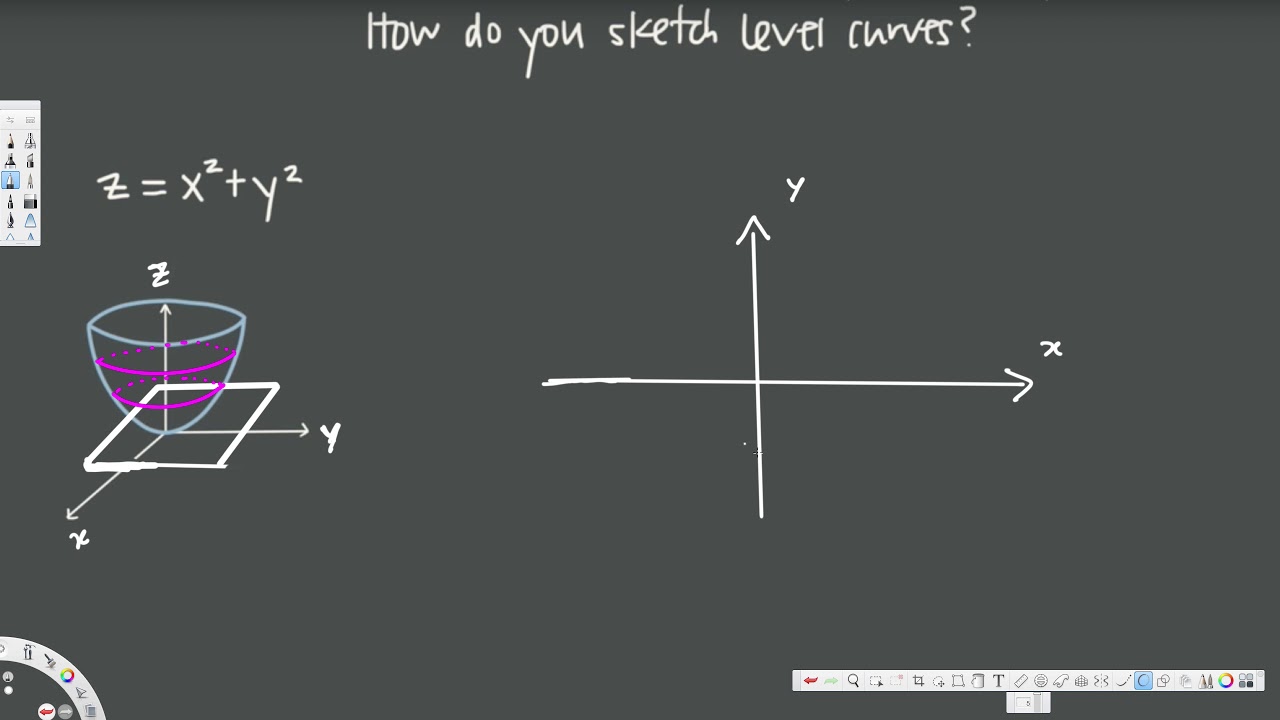


How Do You Sketch Level Curves Of Multivariable Functions Vector Calculus 1 Youtube



Math 2110 Section 13 1 Level Curves And Level Surfaces Youtube



14 1 Functions Of Several Variables Mathematics Libretexts
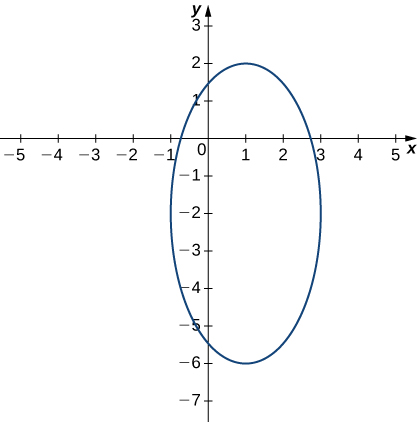


Functions Of Several Variables Calculus
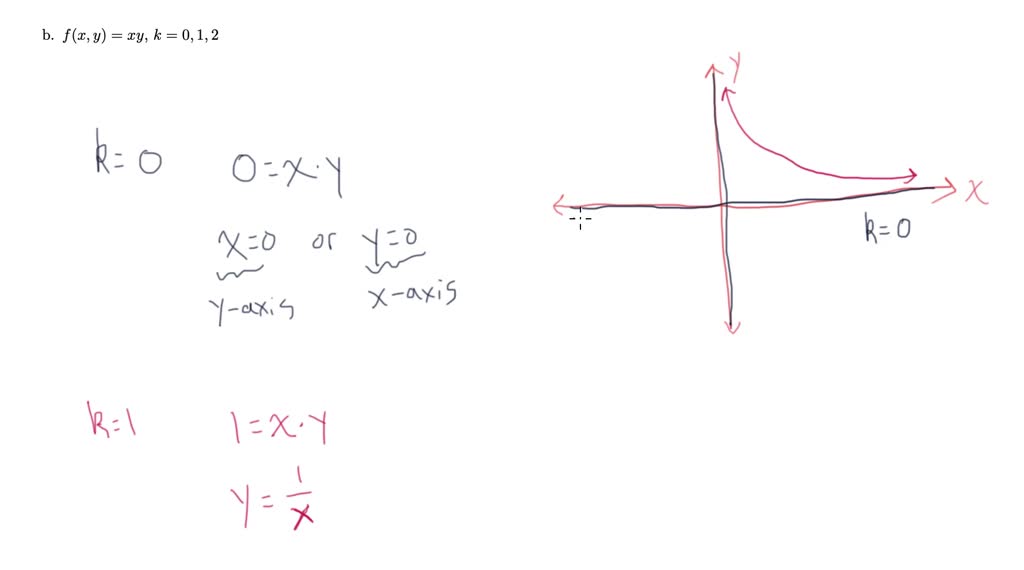


Level Curves And Surfaces Example 1 Numerade
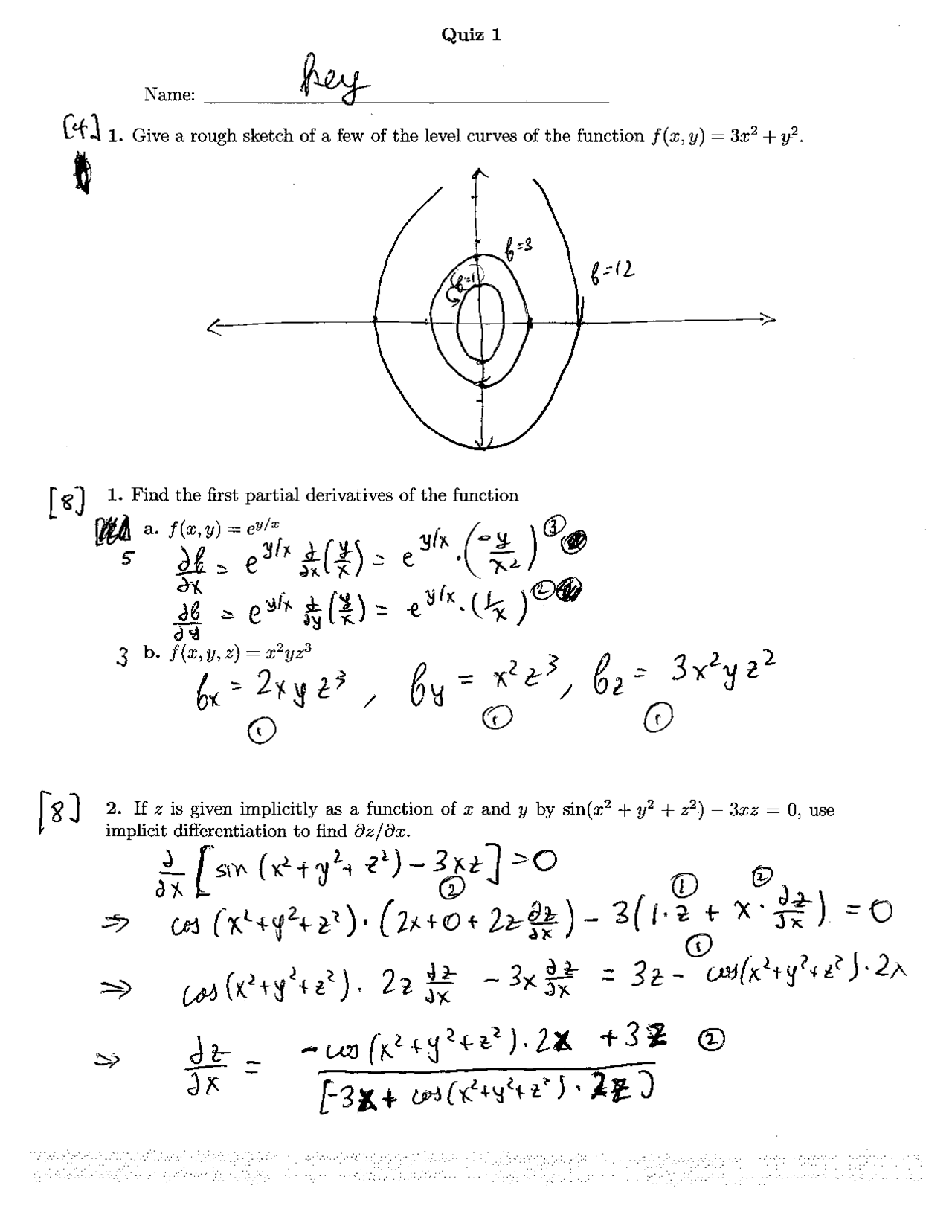


Solution Of 3 Problems On Calculus And Analytic Geometry I Quiz 1 Math 2443 Docsity



Level Curves Of Functions Of Two Variables Youtube



Multivariable Functions Application Center



Calc 3 Calculating The Volume Between Two Non Intersecting Spheres 1st Is Problem And 2nd Is My Work Done Spot Any Errors Calculus
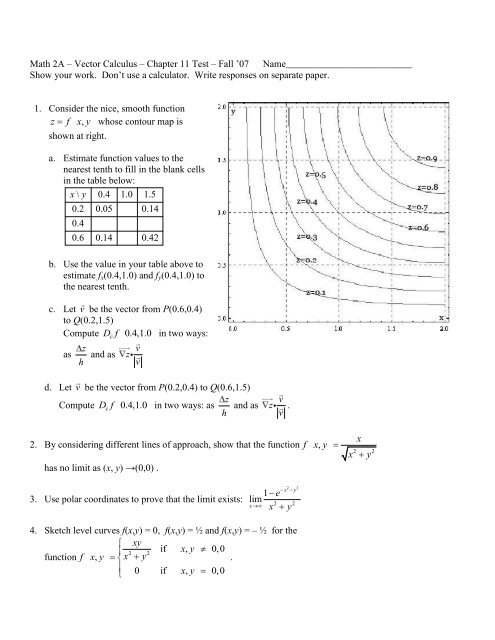


Math 2a A Vector Calculus A Chapter 11 Test Geofhagopian Net
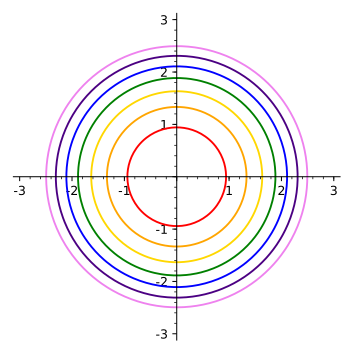


14 1 Functions Of Several Variables


The Gradient And Directional Derivative



Calculus 3 Lecture 13 1 Intro To Multivariable Functions Domain Sketching Level Curves Youtube



Solved Chapter 13 Worksheet 1 Math 4a Multivariable Ca Chegg Com


Level Sets Ximera



How To Draw A Contour Map Calculus Maps Catalog Online



Answered 1 Find The Domain And Two Level Curves Bartleby


12 1 Introduction To Multivariable Functions Mathematics Libretexts



Level Sets Math Insight
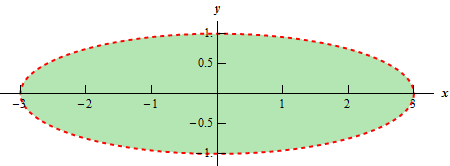


Calculus Iii Functions Of Several Variables
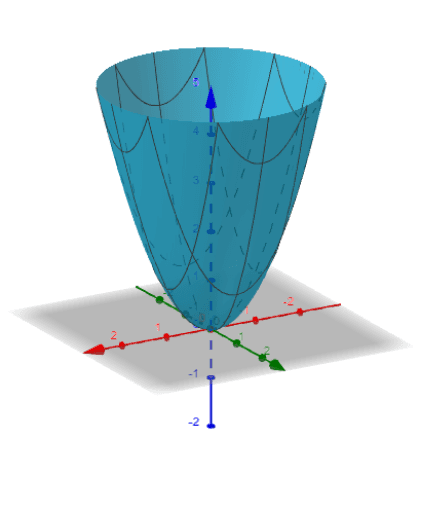


Calc 3 Summer 19 Geogebra



Calculus 3 Tangent Line To Level Curve Youtube
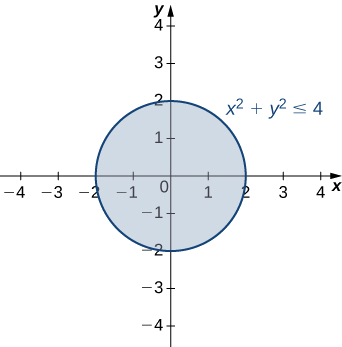


14 1 Functions Of Several Variables Mathematics Libretexts
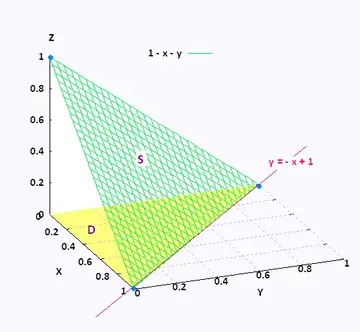


Oql1pw9xmctx6m
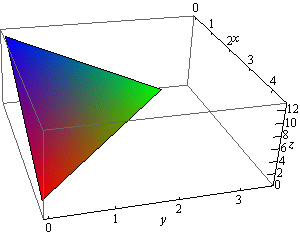


Calculus Iii Functions Of Several Variables



Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



Calculus Iii 2210 4 Sample Midterm Exam 2 Exam Date 4 November 05 Name
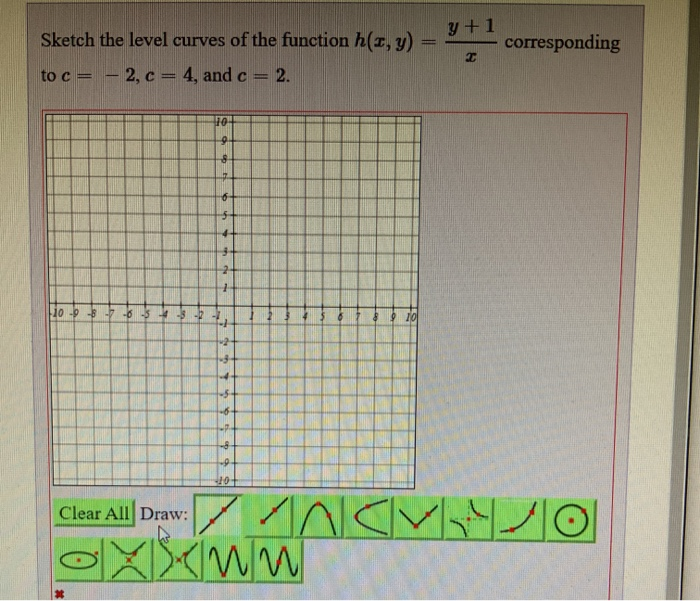


Solved Corresponding Sketch The Level Curves Of The Fun Chegg Com



0 件のコメント:
コメントを投稿