2^x 3^y = z^2 1 where x, y, and z are nonnegative integers We can see that 1 is a congruence modulo 8 3^y = z^2 (mod 8) 2 When z=1 and and y=2 we have 3^2 = 1 (mod 8) 3 and by Fermat's theorem So this means that y must be even As y is even, we can write y = 2k for some integer k So we have 3^2k 2^x = z^2 z^2 3^2k = 2^xConsider x 3 y 3 z 3 − 3 x y z as a polynomial over variable x Find one factor of the form x^ {k}m, where x^ {k} divides the monomial with the highest power x^ {3} and m divides the constant factor y^ {3}z^ {3} One such factor is xyz Factor the polynomial by dividing it by this factorA classic way to prove inequalities is using AMGM inequality But my approach is different Here's my proof According to an algebraic identity, mathx^3 y^3 z

If X Y Z 0 Then Prove That X3 Y3 Z3 3xyz Youtube
(x y)^3 (y z)^3 (z x)^3-3(x y)(y z)(z x)=2(x^3 y^3 z^3-3xyz)
(x y)^3 (y z)^3 (z x)^3-3(x y)(y z)(z x)=2(x^3 y^3 z^3-3xyz)-` X ` Y Z =` 33X ` ` ` Z = 5 ` X 2Y Z =` 3 ` Here are the seven steps 1 Pick a letter (If one of the equations has only two letters, choose the ` `letter that is missing) 2 Pick an equation that contains that letter 3 Solve for that letter in that equation 4 Substitute what you get into any other equations that contains that letter, ` `and simplify 5 Now you have only twoGroup 2 (yz) • (x 3) Group 3 (xy) • (z 3) Looking for common subexpressions Group 1 (xz) • (y 3) Group 3 (xy) • (z 3) Group 2 (yz) • (x 3) Bad news !!




Solution Manual For Engineering Electromagnetics 8th Edition By Hayt By A Issuu
x^4y^4z^4 = 25/6 Given { (xyz=1), (x^2y^2z^2=2), (x^3y^3z^3=3) } The elementary symmetric polynomials in x, y and z are xyz, xyyzzx and xyz Once we find these, we can construct any symmetric polynomial in x, y and z We are given xyz, so we just need to derive the other two Note that 2(xyyzzx) = (xyz)^2(x^2y^2z^2) = 1 So xyyzzx = 1/2 Note that 6xyz = (xyzIf the polynomial k 2 x 3 − kx 2 3kx k is exactly divisible by (x3) then the positive value of k is ____Simplify (X^2 Y^2)^3 (Y^2 Z^2)^3 (Z^2 X^2)^3/(X Y)^3 (Y Z)^3 (Z X)^3 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 6 Question Bank Solutions 144 Concept Notes & Videos 416 Syllabus Advertisement Remove all ads Simplify (X^2 Y^2)^3 (Y^2 Z^2)^3 (Z^2 X^2)^3/(X Y)^3 (Y Z)^3 (Z X)^3 Mathematics
First, Schur's inequality provides that $$ x^3y^3z^33xyz\ge xy(xy)yz(yz)zx(zx) $$ Then, $$ xy(xy)\ge 2xy\sqrt{xy} $$ and hence $$ x^3y^3z^33xyz\ge 2\big(xy\sqrt{xy} yz\sqrt{yz} zx\sqrt{zx} \big) $$Click here👆to get an answer to your question ️ Using the identity and proof x^3 y^3 z^3 3xyz = (x y z)(x^2 y^2 z^2 xy yz zx) こんばんは。よろしくお願いいたします。x^3y^3z^3=(xyz)(x^2y^2z^2xyyzzx)3xyzになるのどうしてでしょうか。どうぞ、よろしくお願いいたします。 数学 解決済 教えて!goo
Ex 25, 13 If x y z = 0, show that x3 y3 z3 = 3xyz We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0, x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx) x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence pro Find the value of x3 y3 z3 – 3xyz if x2 y2 z2 = and x y z = 15 Given x² y² z² = And x y z = 15 To Find The value of , x³ y³ z³ 3 x y zAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators




Tinkutara Equation Editor Math Forum Question




If X Y Z 0 Show That X3 Y3 Z3 3xyz
Simplifying 3x 1y = z Solving 3x 1y = z Solving for variable 'x' Move all terms containing x to the left, all other terms to the right Add 'y' to each side of the equation 3x 1y y = y z Combine like terms 1y y = 0 3x 0 = y z 3x = y z Divide each side by '3' x = y z Simplifying x = 0 (xy)^3 (yz)3 (zx)^3 = 3(xy)(yz)(zx) That is it no constraints etc It mentions "This can be done by expanding out the brackets, but there is a more elegant solution" Homework Equations The Attempt at a Solution First of all this only seems to hold in special cases as I have substituted random values for x,y and z and they do not agree It seems more like thisOn x^3 x y^3 y = z^3 z Suppose we wish to find an infinite set of solutions of the equation x^3 x y^3 y = z^3 z (1) where x, y, z are integers greater than 1 If z and x are both odd or both even, we can define integers u and v such that z=uv and x=uv Substituting into equation (1) gives y^3 y = 2v(3u^2 v^2 1) Since v divides the righthand side, it would be nice if it




Mathematics Ii Tranquileducation




Ppt Polynomials Powerpoint Presentation Free Download Id
Answer by lenny460 (1073) ( Show Source ) You can put this solution on YOUR website!Finite Math Solve by Substitution 2xyz=3 , 3xy3z=3 , x3y2z=3 2x y − z = 3 2 x y z = 3 , 3x − y 3z = 3 3 x y 3 z = 3 , −x − 3y 2z = 3 x 3 y 2 z = 3 Move all terms not containing y y to the right side of the equation Tap for more steps Subtract 2 x 2 x from both sides of the equationTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Verify that `x^3y^3z^33x y z=1/2(xyz)(xy)^2(yz)^2(zx)^2`




X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Mathematics Topperlearning Com T86qex55



2
Phân tích đa thức thành nhân tử x3 y3 z3 −3xyz x 3 y 3 z 3 − 3 x y z ( Làm rõ từng bước đừng làm tắt giúp mình với nhé ) Theo dõi Vi phạm YOMEDIA Toán 8 Bài 6 Trắc nghiệm Toán 8 Bài 6 Giải bài tập Toán 8 Bài 6Steps for Solving Linear Equation xyz=3xyz x y z = 3 x y z Subtract 3xyz from both sides Subtract 3 x y z from both sides xyz3xyz=0 x y z − 3 x y z = 0 Subtract y from both sides Anything subtracted from zero gives its negation Pascal's (or Tartaglia's) Tetrahedron the left outline is a binomial expansion of $(xy)^3$, while the right outline is a binomial expansion of $(xz)^3$ and the bottom outline is a binomial expansion of $(yz)^3$




If X Y Z 6 And Xy Yz Zx 12 Then Show That X3 Y3 Z3 3xyz Maths Polynomials 12 Meritnation Com




An Inequality With Constraint Xix
Answer The formula of x 3 y 3 z 3 – 3xyz is written as Let us prove the equation by putting the values of x = 1 y = 2 z = 3 Let us consider LHS of the equation LHS = x 3 y 3 z 3 – 3xyz LHS = 1 3 2 3 3 3 – 3 (1 × 2 × 3)Factoring by pulling out fails The groups have no common factor and can not be added up to form a multiplication Final result x 3 y x 3 z xy 3 xz 3 y 3 z yz 3 Why learn this Terms and topics CancelingX^3y^3z^33xyz=(xyz)(x^2y^2z^2xyyzzx)a^3b^3c^33abc=(abc)(a^2b^2c^2abbcca)a^3b^3c^33abc formula proofx^3y^3z^33xyz formula proofa



How Do You Find The Equations For The Tangent Plane To The Surface X 2 2z 2 Y 2 Through 1 3 2 Socratic



Stanleyrabinowitz Com
Chứng minh x^3y^3z^3=3xyz biết xyz=0 Cho xyz=0 CMR x 3 y 3 z 3 =3xyz Theo dõi Vi phạm YOMEDIA Toán 8 Bài 3 Trắc nghiệm Toán 8 Bài 3 Giải bài tập Toán 8 Bài 3 Trả lời (1) Ta có \(xyz=0\Leftrightarrow xy=z\) \(\Leftrightarrow\left(xy\right)^3=\left(z\right)^3\) \(\Leftrightarrow x^33x^2y3xy^2y^3=z^3\) \(\Leftrightarrow x^3y^3z^3=3x^2y3xy^2\Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor The answer is yes, the rational points on your surface lie dense in the real topology Let's consider the projective surface S over Q given by X3 Y3 Z3 − 3XYZ − W3 = 0 It contains your surface as an open subset, so to answer your question we might as well show that S(Q) is dense in S(R) Observe that S has a singular rational point P




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Brainly In



If Math X Y Z 0 Math Then Math X Y Z 3 Y Z X 3 Z X Y 3 Math Quora
(xyz)^3 (x y z) (x y z) (x y z) We multiply using the FOIL Method x * x = x^2 x * y = xy x * z = xz y * x = xyClick here👆to get an answer to your question ️ Factorize x^3 y^3 z^3 = 3xyzVerified by Toppr 27x 3y 3z 3−9xyz =(3x) 3y 3z 3−9xyz =(3x) 3y 3z 3−3×3x×y×z using identity a 3b 3c 3−3abc=(abc)(a 2b 2c 2−ab−bc−ca) Putting a=3x,b=y,c=z =(3xyz)(9x 2y 2z 2−3xy−yz−3zx)




1 なんですけど なんでいきなりこの式が出てくるんですか 友達に聞いても Clearnote




Uncategorized Shashank Tutorial
If y=3x and z=2y, what is xyz in terms of x ? What must be subtracted from 4x^42x^36x^22x6 so that the result is exactly divisible by 2x^2x1?Y=xz/3 Simple and best practice solution for y=xz/3 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it Equation SOLVE Solution for y=xz/3 equation x in (oooo) y



X3 Y3 Z3 3xyz Formula Proof
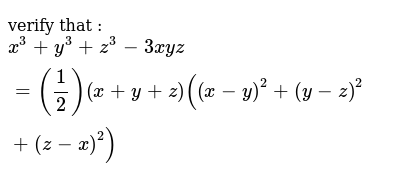



Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2
Consider x 3 y 3 − z 3 3 x y z as a polynomial over variable x Find one factor of the form x^ {k}m, where x^ {k} divides the monomial with the highest power x^ {3} and m divides the constant factor y^ {3}z^ {3} One such factor is xyz Factor the polynomial by dividing it by this factorA 10x B 9x C 8x D 6x E 5x Practice Questions Question 9 Page 148 Difficulty easyClick here👆to get an answer to your question ️ If x y z = 8 and xy yz zx = , find the value of x^3 y^3 z^3 3xyz




Rd Sharma Solutions For Class 7 Maths Chapter 7 Algebraic Expressions Updated For 21 22 Coolgyan Org



2
You can quite easily reduce this system to a single cubic equation However, solving a general cubic equation is not simple To reduce the system, you should read up on Newton's identities What you call a, b, c they call p1, p2, p3 The Cubic fun Answer Given ( x y) 3 ( y z ) 3 ( z x ) 3 3 ( x y )( y z )( z x ) = 2 ( x 3 y 3 z 3 3xyz) Taking LHS ( x y ) 3 ( y z ) 3 ( z x Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange




Solved If X Y Z 3 And Xy Yz Zx 18 Then What Is The Value O Self Study 365




Solved If X Y Z 6 And Xy Yz Zx 11 Then What Is The Value Of X 3 Y 3 Z 3 3xyz
Click here👆to get an answer to your question ️ If x y z = 0 , show that x^3 y^3 z^3 = 3xyz Join / Login Question If x y z = 0, show that x 3 y 3 z 3 = 3 x y z Easy Open in App Solution Verified by Toppr x y z = 0 we know that x 3 y 3 z 3 − 3 x y z = (x y z) (x 2 y 2 z 2 − x y − y z − z x) then ⇒ x 3 y 3 z 3 − 3 x y z = 0 ⇒ x 3 yI don't know what you really want to ask , but here is at least a bit of content to this for this formula Since it is homogenous in x,y,z (so all terms have equal degree), you can read it as a description of a object of algebraic geometry eitherGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz With Video



If 1 X 1 Y 1 Z 0 And X Y Z 9 Then What Is The Value Of X 3 Y 3 Z 3 3xyz Quora
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor prove that (xy)3(yz)3(zx)33(xy) (yz) (zx) =2(x3y3 z 3 3xyz) Maths Polynomials Using identity a 3 b 3 c 3 3abc = (abc)(a 2 b 2 c 2 abXyz=6, 2xyz=3, 3xz=0 \square!




Example 32 Show That Determinant 2xyz X Y Z 3 Class 12



If X Z 225 And Y 226 Then What Is The Value Of X Y Z 3xyz Quora
Factor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y (x−y)(x2 xyy2) ( x y) ( x 2 x y y 2)




Polynomials Ppt Video Online Download
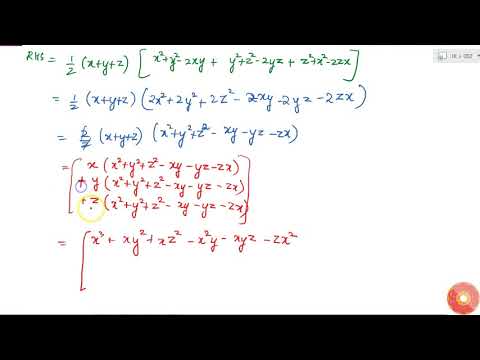



Verify That X 3 Y 3 Z 3 3x Y Z 1
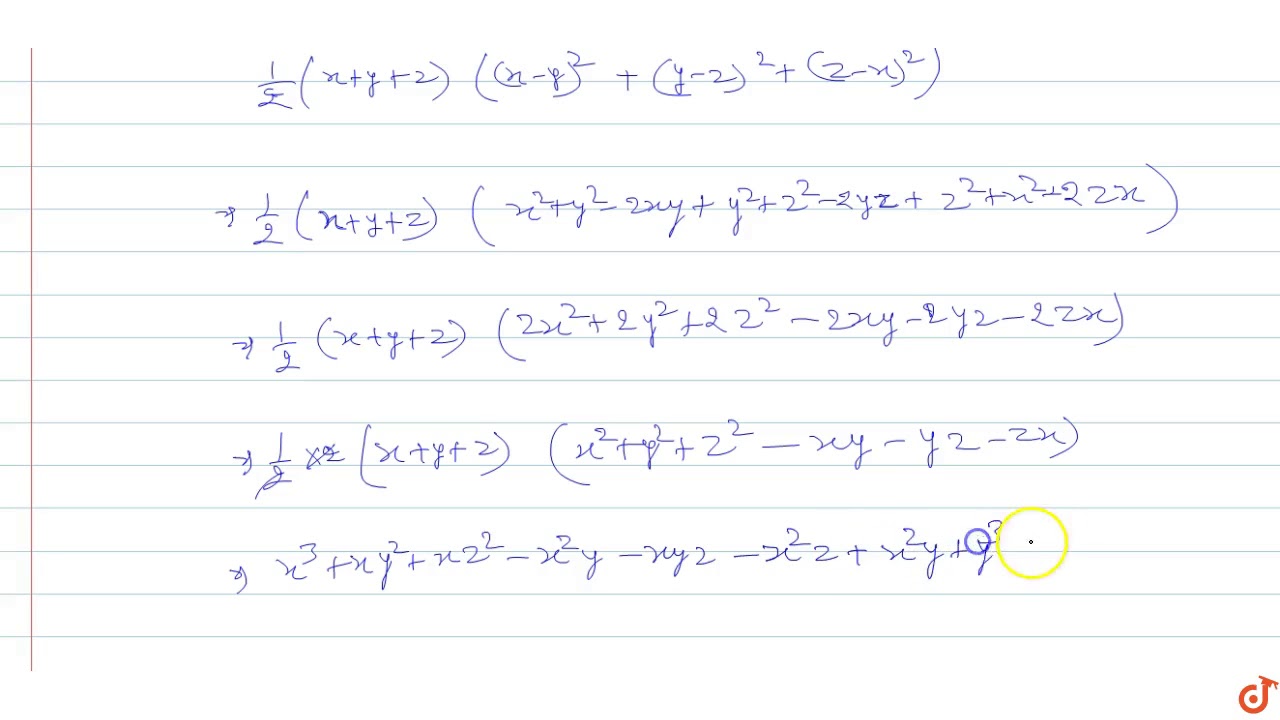



Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




Polynomials Ppt Video Online Download




Vector




Vector




Prove That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Brainly In
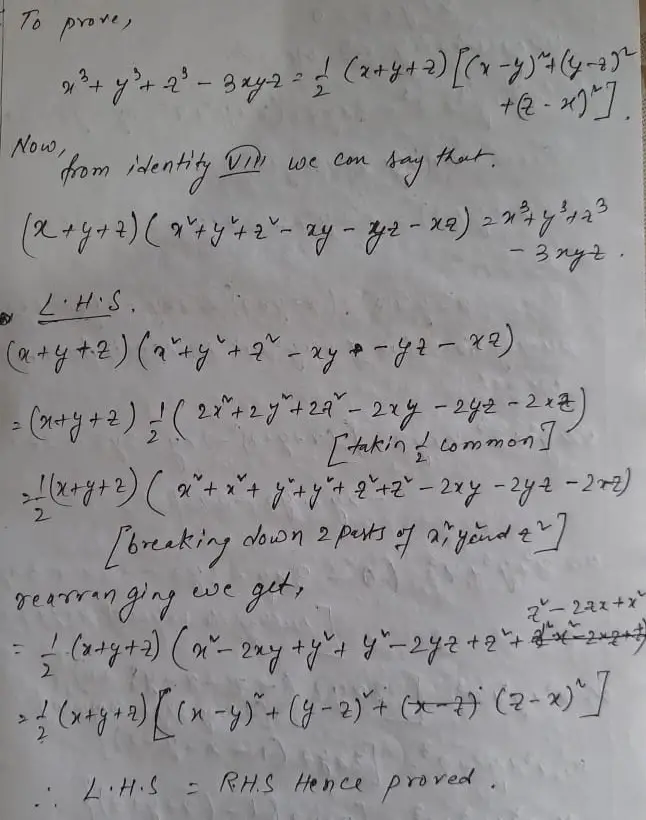



Telangana Scert Class 9 Math Solution Chapter 2 Polynomials And Factorisation Exercise 2 5




X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Proof It Lhs To Rhs Brainly In




If X Y Z Are Positive Integers Then Value Of The Expression X Y Y Z Z X Is A 8xyz B 8xyz C 8xyz D 4xyz Dronstudy Questions




Solved Verify That X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z Z X 2



2




Solved Evaluate Xyz Dx Dz Dy Evaluate Z Dx Dy Dz Where Chegg Com
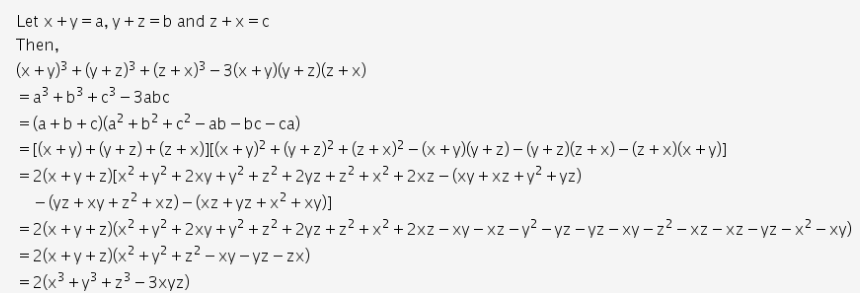



X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Cbse Class 9 Maths Learn Cbse Forum




上 Xy Y2 X X X Y Y X 3 Y 3 X Y X 2 Xy Y 2




If X Y Z 9 And Xy Yz Zx 23 Find The Valure Of X3 Y3 Z3 3xyz



2




3 Jacobians Of Implicit Functions Pdf Differential Equations Elementary Mathematics




Giải Toan Tren Mạng Giup Toi Giải Toan Hỏi đap Thảo Luận Về Toan Học Học Trực Tuyến Olm




Show That X3 Y3 Z3 3xyz X Y Z X2 Y2 Chegg Com




If X Y Z 1 X Y Y Z Z X 1 And X Y Z 1 Find The Value Of X 3 Y 3 Z 3dot Youtube




Ex 2 5 Q No 12 Verify X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




If X Y Z 6 And Xy Yz Zx 11 And Xyz 6 Is Given Find The Value Of X 3 Y 3 Z 3



Using Properties Of Determinants Prove That X Y Z X 2 Y 2 Z 2 X 3 Y 3 Z 3 Xyz X Y Y Z Z X Sarthaks Econnect Largest Online Education Community




Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5



1




X Y Z 3 Y Z X 3 Z X Y 3 X Y Z 3 24xyz Mathematics Stack Exchange



If X 2 Y 2 Z 2 2 X Y Z 3 What Is The Value Of 2x 3y 4z Quora




Ieep2 Advanced Engineering Mathematics Meg801 1 Uniport Studocu




File




Solution Manual For Engineering Electromagnetics 8th Edition By Hayt By A Issuu



2




If X Y Z 0 Then Prove That X3 Y3 Z3 3xyz Youtube




Please Solve The Assignment Attached Find 6 Answers Solutions Learnpick Resources



Pplato Basic Mathematics Gradients And Directional Derivatives



2



Solved Use The Transformation U X Y V Y Z W X Z To Find The Volume Of The Region In The First Octant That Is Enclosed By The Hyperbolic Cylinders X Y 1 X Y 2 Y Z




Verify That X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Class 9th Ex 2 5 Question 12 Youtube




Some Strong Sufficient Conditions For Cyclic Homogeneous Polynomial Inequalities Of Degree Four In Nonnegative Variables Pdf Free Download




Example 32 Show That Determinant 2xyz X Y Z 3 Class 12



X2 Y2 Z2 Formula



Iqqkmssbvdhd1m



Using The Properties Deteminants 3x X Y X Z X Y 3y Z Y X Z Y Z 3z Studyrankersonline
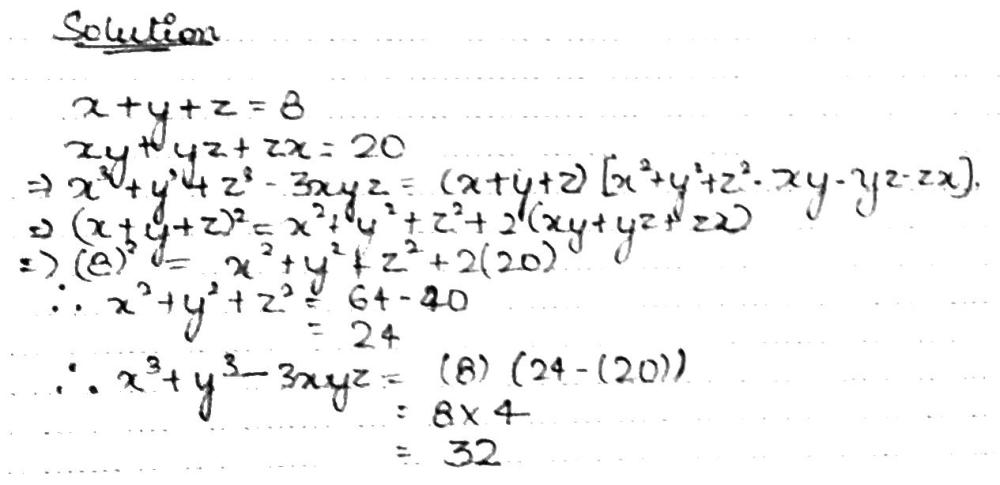



If X Y Z 8 And Xy Yz Zx Find The Value Of X 3 Y 3 Z 3 3xyz Snapsolve



2




Polynomials Ppt Video Online Download




Using Identity Viii X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Solve The Following Question 8x3 Y3 27z3 18xyz Maths Polynomials Meritnation Com




Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials



X Y Z 2 Formula




5 Pts B Use Implicit Differentiation To Find Z If Yz Ln X Z I Homeworklib
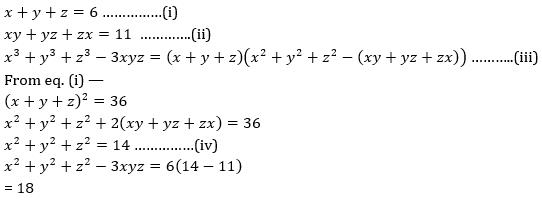



Mathematics Mock Test 4 100 Questions Mcq Test




Solved In Problems 19 Through 24 Find Partial Differential Chegg Com



2




Matt Enlow A Perennial Favorite Reared Its Head Again In Class Today If X Y Z 1 X Y Z 2 And X



2




Implicit Differentiation Advanced Example Video Khan Academy



Find Div Vector F And Curl Vector F Where Vector F Grad X 3 Y 3 Z 3 3xyz Sarthaks Econnect Largest Online Education Community




Polynomials Exercise 2 5 Pocket Gyan




Prove That X Y Y Z Z X 3 X Y Y Z Z X



If X Y Z 6 And Xy Yz Zx 10 Then What Is The Solution Of X 3 Y 3 3xyz Quora




Algebraic Identities Of Polynomials A Plus Topper
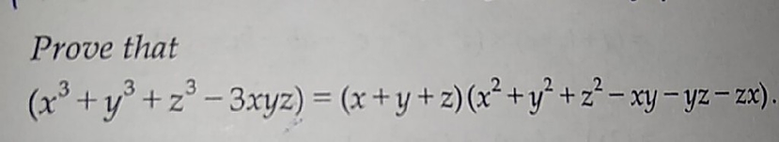



X 3 Y 3 Z 3 3 X Y Z X Y Scholr



2



Using Properties Of Determinants Prove That 3x X Y X Z X Y 3y Z Y X Z Y Z 3z 3 X Y Z Xy Yz Zx Sarthaks Econnect Largest Online Education Community




If X Y Z 9 Amp Xy Yz Zx 23 Then The Value Of X 3 Y 3 Z 3 3xyz Brainly In



Lhsmathleague Weebly Com



How To Solve If X Y Z 0 Find The Value Of Y Z 2 Yz Z X 2 Zx X Y 2 Xy Mathematics Topperlearning Com 7bcu50oo




Rut Gọn Phan Thức X 3 Y 3 Z 3 3xyz X Y 2 Y Z 2 Z X 2 Toan Học Lớp 8 Bai Tập Toan




How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube




Ppt Polynomials Powerpoint Presentation Free Download Id




Verify X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 And Then Factorize 64x3 125y3 64z3 240xyz Brainly In




印刷可能 X 3 Y 3 X 3 Y 3 Identity



Using The Properties Of Determinants Y Z Z Y Z Z X X Y X X Y 4xyz Studyrankersonline




A If X 3 Y 3 Z 3 3 X Y Z And X Y Z 0 Find Frac X Y 2 X Y Frac Y Z 2 Y Z Frac Z X 2 Z X




सत य प त क ज ए X 3 Y 3 Z 3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2




X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube




Mathematics Cbse Mtg Champion 12th Class Flip Book Pages 101 150 Pubhtml5




26 Prove That X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X Maths Polynomials Meritnation Com



2




New Question Verify That X3 Y3 Z3 3xyx 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Tex Textless H2 Brainly In



0 件のコメント:
コメントを投稿